Labyrinth
Contents
Problem Description
* Input Predicates: field/2, init_on/2, goal_on/2, connect/3, max_steps/1
* Output Predicates: push/3
Ravensburger's Labyrinth game deals with guiding an avatar through a dynamically changing labyrinth to certain fields. The labyrinth is represented by a quadratic board whose fields can (but do not have to) be connected in the four cardinal directions. The shape of the labyrinth changes over time as its rows and columns can be pushed either horizontally or vertically, which involves moving fields out of and into the board. To get to another field, in each turn, the avatar can follow paths that starting from the avatar's location traverse pairwisely connected fields.
We here consider a variation of the original game in which:
- The field of the labyrinth pushed out of the board (possibly hosting the avatar) immediately returns into the board (possibly with the avatar still residing on it) on the other end of the pushed row or column, respectively.
- After a push, the avatar can move to any field reachable via a path in which every (non-terminal) field has a connection to its successor, and vice versa. (Note that there always is a path to a field the avatar already resides on.)
- There is a unique starting and a unique goal field in the labyrinth.
- A solution is represented by pushes of the labyrinth's rows and columns such that the avatar can from its starting field (which changes its location when pushed) reach the goal field (which also changes its location when pushed) by a move along some path after each push.
- There is a maximum number of pushes, and the avatar must be able to reach the goal field (which can be relocated by pushes) by moving along some path after each push.
Input format
The fields of a quadratic NxN-labyrinth are provided by instances of predicate "field" as follows:
field(1,1). field(1,2). ... field(1,N). field(2,1). field(2,2). ... field(2,N). ... field(N,1). field(N,2). ... field(N,N).
The starting and the goal field are specified by exactly one instance of "init_on" and exactly one instance of "goal_on":
init_on(x_i,y_i). goal_on(x_g,y_g).
It always holds that 1 ≤ x_i,y_i,x_g,y_g ≤ N.
The connections of fields are given by instances of "connect" looking as follows:
connect(x,y,d).
Again, we have 1 ≤ x,y ≤ N. Furthermore, direction d can be "n" for north, "s" for south, "e" for east, or "w" for west.
Finally, the maximum number of pushes is determined by exactly one instance of "max_steps":
max_steps(m).
Argument m is a positive integer.
An exemplary input for the above example looks as follows:
field(1,1). ... field(1,4). .... field(4,1). ... field(4,4). init_on(3,2). goal_on(1,4). connect(1,1,s). connect(1,1,w). connect(1,2,n). connect(1,2,e). connect(1,2,w). connect(1,3,e). connect(1,4,n). connect(1,4,w). ... connect(4,4,w). max_steps(2).
Output format
A solution (as described above) is represented by instances of "push":
push(z,d,s).
In an instance, direction d is one of "n" for north, "s" for south, "e" for east, or "w" for west, indicating that the row (if d="e" or d="w") or column (if d="n" or d="s") z is pushed into direction d. It must hold that 1 ≤ z ≤ N, where NxN is the board size. Furthermore, step number s expresses that the push happens after pushes 1,...,s-1 (and possible moves of the avatar along paths). The sequence of pushes is consecutive, that is, there are t instances of "push" for step numbers 1,...,t, where t ≤ m for maximum number m of pushes. Note that t < m (and even t = 0) is allowed, but the avatar must be able to reach the goal field by moves possible after the performed pushes.
The two alternative solutions for our example above are represented as follows:
Solution A: push(1,w,1). push(3,s,2).
Solution B: push(1,w,1). push(2,n,2).
Example
For illustration, consider the following labyrinth on a 4x4-board:
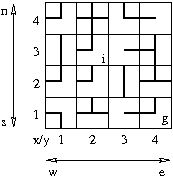
We count rows x vertically from the bottom to the top, and columns y horizontally from the left to the right. The connections of the labyrinth's fields are indicated by lines from the center of a field to the field's border, each connection running in one of the four cardinal directions: "n" for north (upwards), "s" for south (downwards), "e" for east (rightwards), and "w" for west (leftwards). For instance, the field located at (1,3) has a single connection to the east, while the field at (3,4) has three connections running to the north, south, and west. Finally, the avatar is initially located at (3,2), and the goal is to reach the field at (1,4). Assuming a limit of two pushes, there are the following two solutions:
Solution A
The first solution is shown below, providing the initial setting (left part) along with the situations encountered after the first (center part) and second (right part) push. The pushes are indicated by arrows pointing to the pushed row or column, respectively:
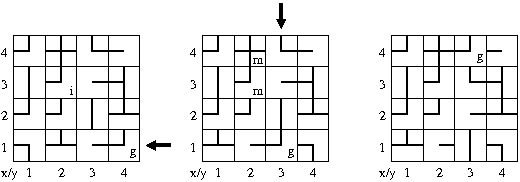
The first step consists of pushing row 1 to the west. Observe that the field at (1,1) before the push reappears at (1,4) after the push, and also the goal field changes its location from (1,4) to (1,3). In the resulting labyrinth configuration, there are paths from the initial field, still at (3,2), to itself as well as to (4,2). The avatar can move to either one of these two fields to reach the goal field after the next push. (But recall that we are interested only in a sequence of pushes that admits reaching the goal field by some moves, but not in the moves themselves.) In the second step, we push column 3 to the south, so that the goal field reappears at (4,3), which can then be reached by a path both from (3,2) and (4,2).
Solution B
The second solution is presented in the same fashion as the previous one:
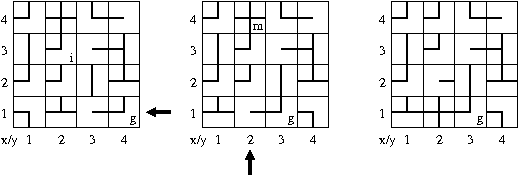
Again, the first step is to push row 1 to the west. (Afterwards, the avatar must move to the field at (4,2) to reach the goal after the second push, but this move does not belong to the solution.) In the second step, column 2 is pushed to the north, so that the field at (4,2) reappears at (1,2). From there, the avatar has a path to the goal field, which has been pushed to (1,3) before. Finally, note that the second push is necessary even if the field at (1,2) in the middle configuration had a connection to the south (touching the lower border of the board) because the legal moves of the avatar are along paths inside the board, not going out of and back into it. Hence, the transition from (4,2) to (1,2) can only be achieved by a second push, but not by any move.
Author(s)
Author: Martin Gebser
Affiliation: University of Potsdam