RESEARCH

My research activity focus  on two areas:

1. Numerical Analysis;
2. Mathematics Education.

In the Numerical Analysis field my research activity focused on the study of special polynomial of interest in the field of interpolation and of differential equations. More precisely, it is provided a new definition of the classical Lidstone polynomials; this definition, given in determinantal representation, allows to deduce the most important properties of the previous polynomials through elementary notions of linear algebra.

Moreover, they are considered new boundary conditions for the differential equation 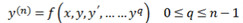 and it is shown that the related boundary value problem has a unique solution. Afterwards, it is proposed  a constructive proof of the solution of the problem and it is also given a numerical procedure for its computation.

Part of this research was the following academic honor:

The Best Paper Award of The World Congress on Engineering (WCE) 2007, London U.K.

Paper Title: No Classic Boundary Conditions.

The area of interest [2] has been my primary research interest over the last decade.

In fact, the Computer Aided Mathematics Education is a field of great current interest whose results have a determining influence on the teaching and therefore on future development of Mathematics. Designing software more powerful, such as MatLab and Mathematica, are undermining the traditional teaching methods and contents.

More precisely, my research pertains to the three-dimensional theoretical, historical and epistemological and experimental processes of mathematics teaching-learning, by marking more on experimental one, that is, in the verification field of the transformations inherent the methods of construction and sharing math knowledge: consider what actually happens in the teaching-learning with the computer through programming environments adapted to the age of learners.

Based on the results achieved more research areas have resulted such as:

• approach to the mathematical modeling with the computer;
• methodological approaches for the coordination of both theoretical and algorithmic methods in order to encourage the display of mathematical phenomena;

that even though distinct for clarity reasons, however, should not be seen as opposing or without intersections, but complementary and often intertwined both from a methodological and theoretical point of view.

My work on programming also includes the study and the realization of particular algorithms regarding the construction of algebraic curves, (that, usually, are treated in university courses, only through different types of equation (Cartesian, parametric and polar) as well as models and simulations.

Future plans

My future plan of research focus more on the verification of the role that mathematics must have in the training of young people in the current socio-historical moment.

In other words the main question is: what is the Mathematics to teach and/or to learn, such as methods and tools?

No one can deny the power, the spread and the inevitability of modern technological tools that are able to perform, or to support an increasing "quantity of Mathematics".

The massive use of these tools requires a serious updating of traditional curricula of mathematics education, as well as the used methodologies. From the technical point of view, the use of computers solves an increasing amount of mathematical problems, then you can’t refuse their contribution; on the training, or on the logic-sequential capacity language and intuition need to evaluate and compare the contribution coming from the methods used in the curricular-traditional activity of Mathematics teaching, with what can, instead, come from a more algorithmic and computer programming varying part of the curricula of mathematical contents.